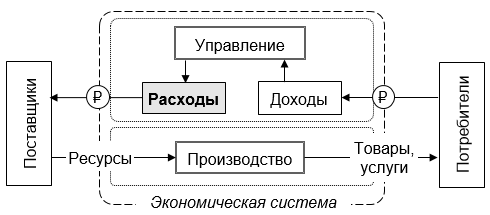
В теории и практике управления современными экономическими системами принято считать, что основные управленческие решения принимаются там и тогда, где и когда расходуются денежные средства.
Как правило расходы опережают реальный процесс получение результата. » — А можно утром стулья, а вечером деньги? — можно, но деньги вперед»
Энтропийный подход к анализу неравномерности распределений денежных средств в рамках управленческих решений позволяет изучать распределения денежных средств здесь и сейчас.
