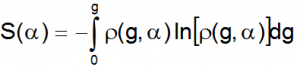Известно, что энтропия является мерилом числа различных микросостояний системы, которым может быть реализовано данное макросостояние, характеризующееся в нашем случае индикатором соразмерности α. Причем, при известной плотности распределения вероятностей ρ(g,α) (4) энтропия может быть рассчитана по стандартной формуле:
Принципиально важен факт наличия максимума. Однако, значение α≈1,84 не соответствует особенности формулы плотности распределения вероятностей ρ(g,α) в точке α=2.0 Кроме того, теоретическая особенность ρ(g,α) при α=2, согласуется с целым рядом фактов анализа распределений в различных экономических системах (Крянев, и др., 2007).
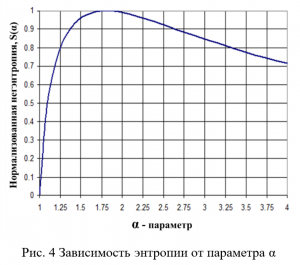
Таким образом, расхождение в положениях максима может указывать на то, что прямое использование понятия энтропии в практических целях для оценки состояния сложной экономической системы может оказаться не вполне корректным. В этой связи заменим понятие энтропии на понятие адаптационной вариативности, используя тот факт, что по определению. Замена энтропии на вариативность позволяет использовать вариативность системы V(α) как метрику способности системы адаптироваться к изменяющимся условиям, поскольку по определению энтропия является значением числом различных микросостояний, которым может быть реализовано данное макросостояние с индикатором соразмерности α.
По видимому, в целях практического применения целесообразно ввести более простую феноменологическую формулу расчета вариативности (9), сохраняющую подобие формы зависимости энтропии S(α) и хорошо согласующуюся с достаточно широким рядом примеров в части достижения своего максимального значения в точке α=2.0
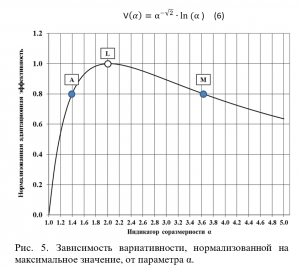
Принимая во внимание, что энтропия во временной развертке имеет тенденцию к росту при неизменных условиях, можно предположить, что введенная в виде ее аналога вариативность сохранит это качество. Соответственно, индикатор соразмерности распределения вкладов будет стремиться к предпочтительному значению α0 =2.0 («L»).То есть, максимальное значение вариативности, которому соответствует оптимальное значение параметра α0, определяет оптимальное распределение ρ(g,α0) вкладов агентов в итоговое максимальное значение целевой функции. Иначе говоря, существует некая «золотая пропорция» между крайними распределениями эффективности агентов сложной системы: полностью равномерным распределением, соответствующим (анархии управления, α=1), и полностью заорганизованным распределением, соответствующим жесткой вертикали управления (диктатуре управления при α→∞).
Вышеуказанная закономерность соответствия максимума вариативность сложной системы максимуму ее целевой функции находится в согласии с развиваемыми в последнее время «ройными технологиями», моделирующими «роевой интеллект» (Swarm Intelligence) (Rzevski, и др., 2014) (Имамутдинов, 2014) [17,18]. Действительно, задача «ройных технологий» – так оптимизировать управление сложной системой, то есть так перераспределить вклады в целевую функцию системы между всеми ее частями. Примером практической реализации ройной технологии, основанной на оптимальном распределении вклада между отдельными агентами экономической системы, служит организация работа таксомоторной компании в Лондоне (Имамутдинов, 2014).
Для жизнеспособной экономической системы в процессе ее функционирования характерны минимальные затраты ресурсов и кратчайшие сроки адаптации к новым условиям. Использование распределения долей с максимумом адаптационной эффективности для управления экономической системой дает большую свободу выбора вариантов принятия управленческих решений и, следовательно, наилучшую возможность адаптироваться к происходящим изменениям. При распределениях близких к равномерному и близких к максимально неравномерному у системы имеются ограниченные возможности для адаптации к изменяющимся внешним условиям, о чем свидетельствует минимальные значения адаптационной эффективности для этих двух крайних типов распределений вкладов (Рис. 5).
В процессе функционирования системы реальное распределение долей вклада отдельных подразделений сложной системы может отличаться от запланированного оптимального распределения, соответствующего максимальному значению адаптационной эффективности. В нашем случае, существование предпочтительное распределение вкладов агентов системы позволяет целенаправленно осуществлять коррекции реальных распределений. (Табл. 1, Табл. 2)
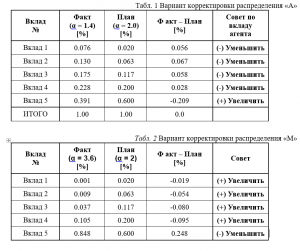
Причем отклонение реальной доли от запланированной, соответствующей «золотой пропорции» для подразделения будет сигнализировать о снижении вариативности состояния системы и, как следствие, ее адаптационного потенциала. Следовательно, постоянный временной мониторинг значений реальных долей может служить инструментом, дающим возможность оперативно принимать управленческие решения по оптимизации её структуры и работы.
Заключение
При исследовании сложных систем с точки зрения их эффективного функционирования может быть два подхода в зависимости от того на какой стадии развития находится система. Если система находится в стадии создания, то необходимо создавать её структуру и взаимодействие её составных частей таким образом, чтобы обеспечивалось оптимальные значения целевой функции системы. Если система находится в состоянии динамического функционирования, то в соответствии с изменением в её работе необходимо в адаптационном режиме управленческих решений поддерживать оптимальную структуру, обеспечивающую оптимальное значение целевой функции. Предложенная в настоящей работе схема, использующая вариативность, дает возможность решать вышеуказанные две задачи.