Энтропия распределений ресурсов как индикатор жизнеспособности экономических систем
Закон необходимого разнообразия (Ashby, 1957) акцентирует внимание специалистов на анализе жизнеспособности различных систем (Докторович, 2015). При этом в качестве метрики разнообразия используется энтропия. Известно, что согласно формуле Больцмана энтропия (H) является функцией от числа различных микросостояний системы (W), которым может быть реализовано макросостояние. В экономике макросостояние системы (домохозяйства, предприятия и т.п.) можно охарактеризовать распределением определенного объема ресурса {GN}={G1, G2, …, GN,} на {N}={n1, n2, …, N} статей с конкретной соразмерностью значений числового ряда {GN}. Последняя визуализируется в виде диаграмм (кривых) Лоренца (Lorentz, 1905) и измеряется с помощью коэффициента Джини или с помощью индикатора соразмерности α. Что касается отличительных признаков микросостояний состояний экономической системы при равенстве значений макропараметров: среднего значения и индикатора соразмерности распределения α, то в их основе лежит приоритетность. То есть, два микросостояния различны, если порядок «привязки» ряда значений {GN}={G1, G2, …, GN,} к перечню позиций {N}={n1, n2, …, N}. Например, вариант А={n1<->G1, n2<->G2,…, N<->GN} не равнозначен варианту B={n2<->G1, n1<->G2, …, N<->GN}. Максимальное число W различных вариантов могут быть N!=1*2*…*N. Однако это число снижается в случае совпадений значений в числовом ряду {GN}. В пределе W=1 при равномерном распределении значений. При этом энтропия равна Ln(1)=0. Не столь очевидно частичное снижение энтропии при реализации групп равных значений в ряду {GN}={G1, G2, …, GN,}. В пределе группа равных значений включает (N-1) элементов и число различных вариантов уменьшается до уровня W=N. Соответствующее значение энтропии пропорционально Ln(N).
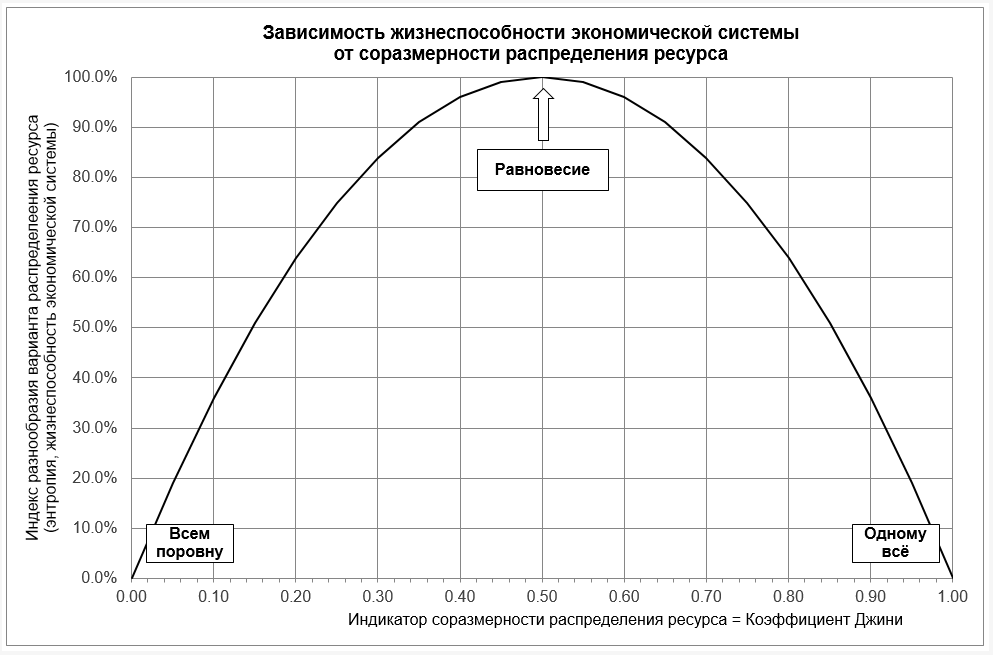 Сопоставляя данные выводы с соразмерностью числового ряда, логично предположить существование максимального значения энтропии экономической системы между двумя упомянутыми предельными случаями.
Сопоставляя данные выводы с соразмерностью числового ряда, логично предположить существование максимального значения энтропии экономической системы между двумя упомянутыми предельными случаями.
Ashby W. Ross An Introduction to Cybernetics [Книга]. — London : CHAPMAN & HALL LTD, 1957. — SECOND IMPRESSION : Т. I.
Lorenz M. O. Methods of Measuring the Concentration of Wealth [Статья] // Publications of the American Statistical Association. — Jun 1905 г.. — 70 : Т. 9. — стр. 209-219.
Докторович А. Б. Разнообразие и сложность жизнеспособной системы [Статья] // Пространство и время. — 2015 г. — Т. 3 (21). — стр. 86-91.
