Простейшей и наиболее распространенной формой оформления числовых рядов, используемых в качестве исходных данных для анализа совокупности расходов, является таблица, состоящая из двух колонок. В левой колонке таблицы приводится название или порядковый номер строки (n), а в правой – значение соответствующего элемента статистического ряда несгруппированных данных (Gn). Данная форма представления может быть трансформирована в иные формы с целью реализации более детального сравнения конкретных свойств экономической системы. На рисунке приведены три формы представления числового ряда {G}={G1, G2,…, GN), позволяющие сравнивать с денежной точки зрения состояния экономических систем в разные моменты времени.
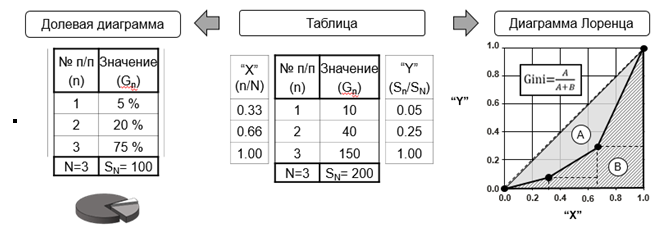
Табличная форма, долевая диаграмма и диаграмма Лоренца позволяют сравнивать числовые ряды как системы:
- с равными количествами строк (N) и равными суммами значений элементов числового ряда (SN);
- с неравными количеством строк (N) и неравными суммами значений числового ряда (SN);
- с любым количествами строк (N) и любыми суммами значений числового ряда (SN).
В первом случае сравнение числовых рядов может быть реализовано простым построчным вычитанием. Поскольку данная форма не предполагает обязательности смысловой однородности элементов числового ряда, то результаты сравнения носят исключительно построчный характер. Кроме того, табличная форма носит открытый характер. То есть, все числа известны.
Во втором случае возникают дополнительные требования к элементам числового ряда. А именно, все элементы должны иметь общий смысл, который позволяет корректно использовать арифметические операции. То есть, например, трансформировать числовые значения в проценты «%»: вес в одной строке/общий вес, длину в одной строке/общую длину, время в одной строке/общее время, денежная единица/сумму, Gn/SN. Таким образом делением на общую сумму реализуется возможность визуального представления неравномерности построчного распределения элементов числового ряда в виде долевой диаграммы.
Таким образом, в методологическом и практическом смысле реализуется возможность количественного сравнения числовых рядов с разными значениями SN и равными N.
К сожалению приходится констатировать часто встречающее некорректное использование долевых диаграмм при разных значениях N, которое может привести к неверным выводам.
Помимо долевой диаграммы при условии однородности смысловой принадлежности строк становятся доступными операции агрегирования (суммирования и вычитания) значений элементов числового ряда, указанных в разных строках таблицы.
Отметим, и еще одну особенность долевой диаграммы. Перевод исходных данных в проценты фактически повышает уровень информационной защиты результатов анализа, поскольку по виду долевой диаграммы нельзя определить абсолютные значения конфиденциальной денежной и управленческой информации.
Однако, при всех достоинствах долевых диаграмм последние не позволяют сравнивать числовые ряды с разными количествами строк N и разными значения сумм SN. Проблема сравнения числовых рядов с разными значениями N и SN решается профильными специалистами использованием диаграмм Лоренца, представляющих числовые ряды в виде кусочно-линейного графика (диаграмма Лоренца). Очевидно, что все диаграммы Лоренца располагаются между равномерным («А» — диагональ квадрата) и существенно неравномерным («М» уголок квадрата) вариантами распределений значений соответствующего числового ряда. Методологические преимущества диаграмм Лоренца расширяются параметром неравномерности в виде коэффициента Джини (Gini), который позволяет упорядочить диаграммы Лоренца в интервале (0.0; 1.0). Однако, коэффициент Джини последний не дает ответа на вопрос о предпочтительности одних числовых рядов над другими. Вопрос о том, чем один числовой ряд «предпочтительней» другого, остается открытым. Ответ на данный вопрос позволил бы изучать динамику различных систем, состояние которых характеризовалось бы конкретным числовым рядом. В этой связи становятся целесообразными попытки поиска нового параметра числовых рядов как аналога энтропии. То есть, если бы удалось рассчитать энтропию состояний системы с характерными числовыми рядами, то предпочтительным было бы состояние с большим значением энтропии. Такая возможность носит характер диагностики, позволяющей упорядочить состояния различных систем и сделать прогноз развития событий. Однако, данная возможность стала бы полноценным практическим инструментом управления системами в случае, если бы удалось сделать обратный ход. А именно, однозначно связать энтропию с табличной формой представления числового ряда. Иными словами так изменить исходный числовой ряд, чтобы увеличить энтропию соответствующей системы. Итак, «золотым ключиком» к реализации возможности диагностики и управления состояниями систем стало бы функциональная связь энтропии и неравномерности распределения значений числовых рядов.

